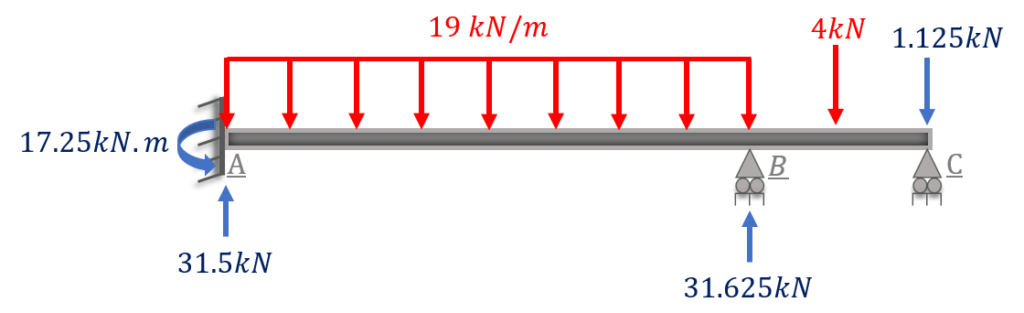
Example 1: Analyze the beam shown in the figure that is subjected to a distributed load and a point force, use the matrix method of stiffness.
EI = Constant
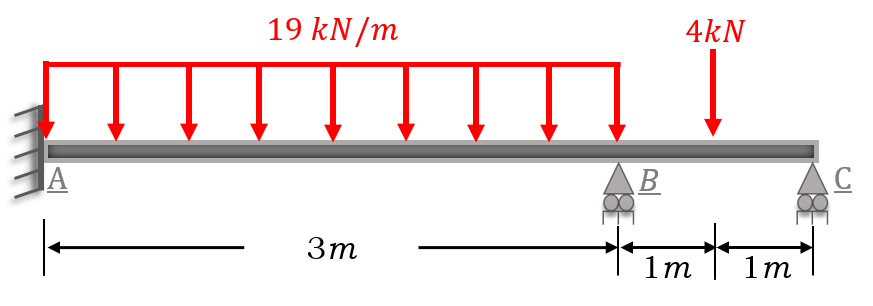
Solution:
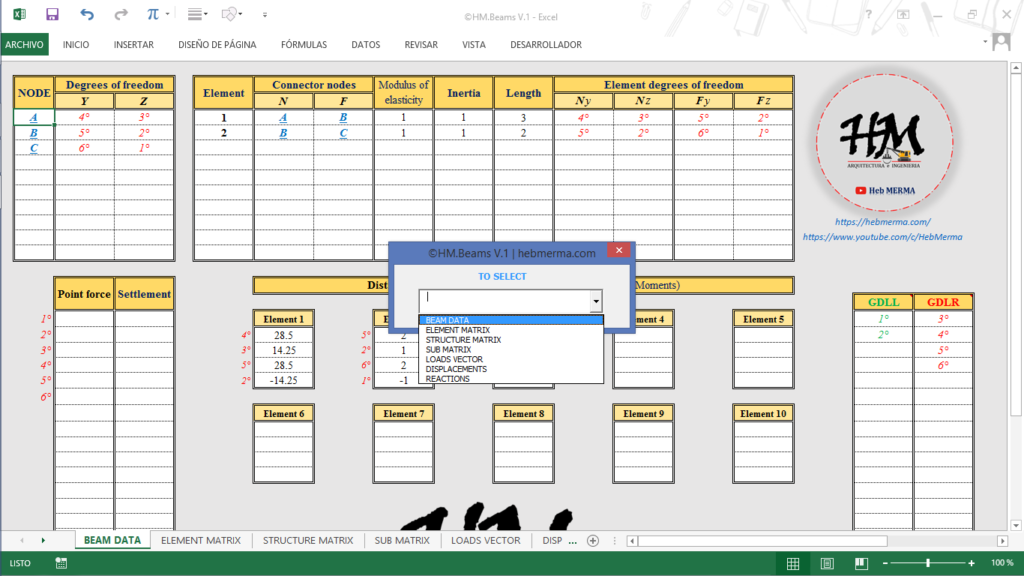
a) Define the degrees of freedom and orientation of the element.
Note:
- The beam is not subjected to axial load, therefore two degrees of freedom are defined at each node (shear and moment).
- First we define the free degrees of freedom (green color).
- Second, we define the restricted degrees of freedom (red color).
- Finally, we define the orientation of the element.
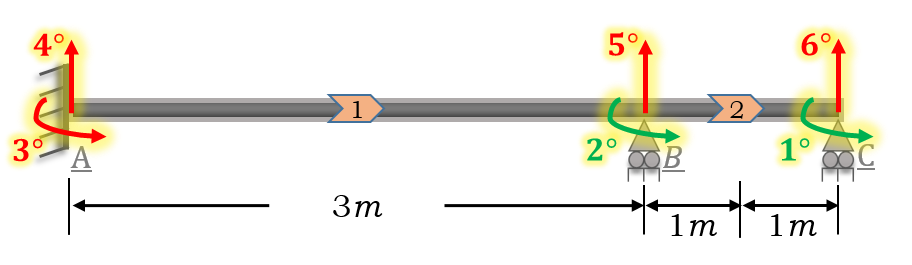
b) Assemble the stiffness matrix of each element.
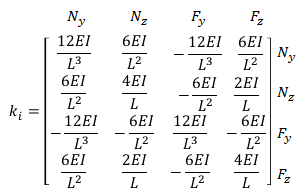
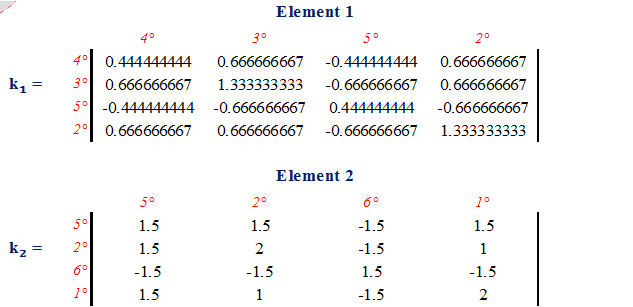
c) Assemble the stiffness matrix of the beam.
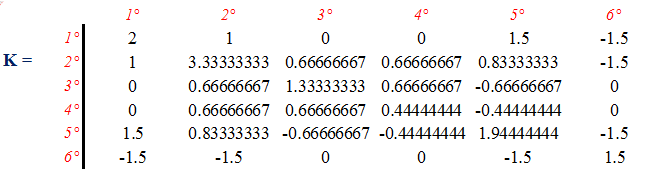
d) Partition of the sub matrix K₁₁.

e) Load vector analysis.
Element 1
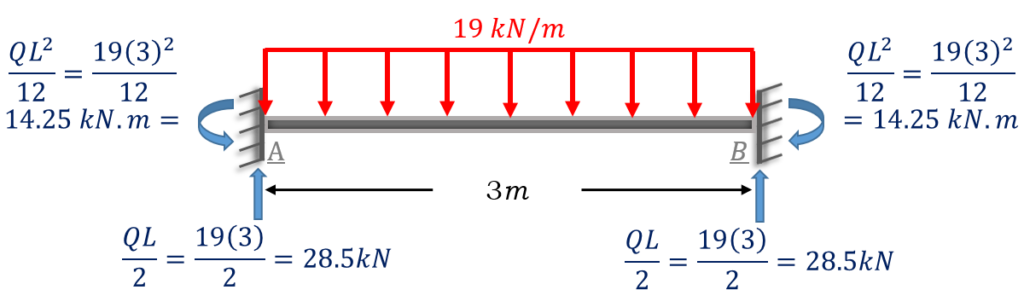
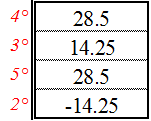
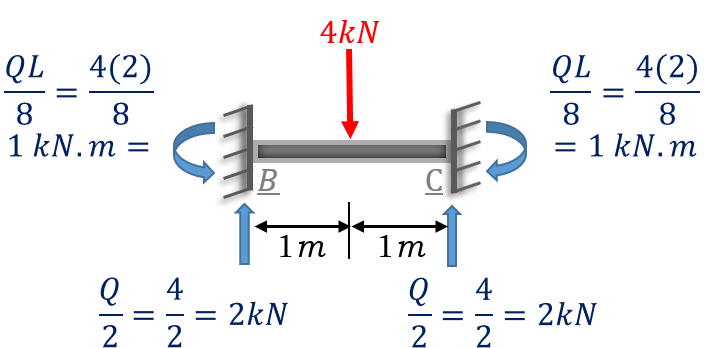
Element 2
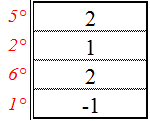

f) Displacement vector calculation. |DD| = |K ₁₁|⁻¹ * |Cc|
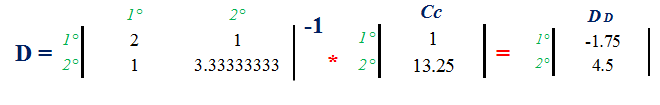
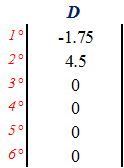
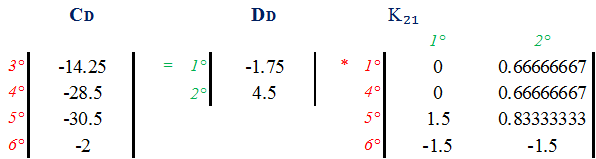
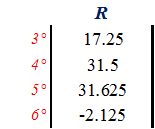
g) Calculation of reactions. |CD| = |DD| * |K₂₁|
WhatsApp reports: +51 992 959 578
