Análisis de Armaduras Espaciales por el Método Matricial de Rigidez | Análisis Estructural | Excel ©HM.Armaduras3D

By: Dr. (c) En I. David Ortiz Soto and Ing. Hebert Luis Merma Taipe

I. Generalidades sobre el método matricial de la rigidez, DSM

DEFINICION:

El Método Matricial de Rigidez, también denominado Método Directo de la Rigidez (DSM) o Método de los Desplazamientos, es un método de cálculo para estructuras isostáticas o hiperestáticas con elementos que se comportan de forma elástica y lineal. Este método se considera como la implementación más sencilla del Método de Elementos Finitos, es útil para calcular el valor de los desplazamientos desconocidos y las reacciones en los soportes con base en la solución de la ecuación matricial de rigidez, y comúnmente está implementado en los programas profesionales de cálculo estructural.

FUNDAMENTO TEORICO:

• Se considera a la estructura como un medio continuo.
• Un sólido deformable es tratado de forma aproximada mediante un número finito de grados de libertad.
• Se emplea la ecuación constitutiva de la elasticidad lineal, que es la Ley de Hooke.

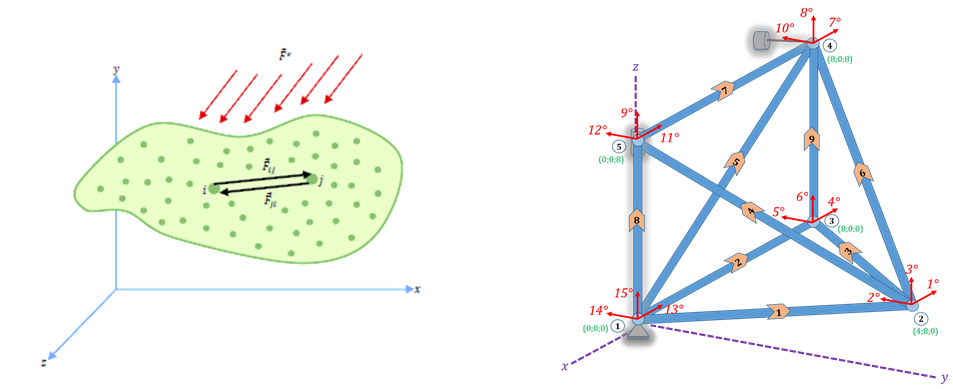
DESCRIPCION DEL METODO:

• Discretizar la estructura y efectuar una notación.
• Calcular la matriz de rigidez de cada elemento en el sistema local y en el sistema global.
• Ensamblar las matrices de rigidez de los elementos para obtener la matriz de rigidez global de la estructura, K.
• Construir el vector de desplazamientos nodales, D.
• Construir el vector de fuerzas nodales equivalentes, F.
• Escribir el sistema de ecuaciones lineales con base en la ecuación matricial de rigidez F=KD.
• Resolver el sistema de ecuaciones. Usualmente este es dividido en dos subsistemas de ecuaciones desacoplados:
  • Subsistema 1. Se calculan los desplazamientos nodales desconocidos.
  • Subsistema 2. Se calculan las reacciones en los soportes.
• Se plantea una ecuación para calcular elementos mecánicos para cada elemento estructural.

II. Aplicación del DSM a Armaduras Tridimensionales

Matriz de rigidez en coordenadas locales para un determinado elemento i de una armadura, ecuación 1-1.

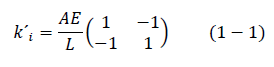
donde

• 𝐴 = área de la sección transversal del elemento
• 𝐸 = módulo de elasticidad del elemento
• 𝐿 = longitud del elemento

Cosenos directores, cos𝜃𝑥, cos𝜃𝑦 y cos𝜃z.  ecuaciones 1-2, 1-3 y 1-4.

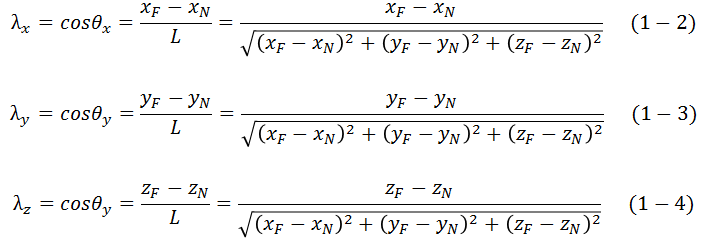
donde

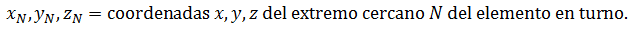
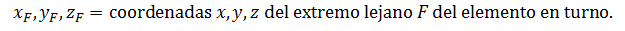
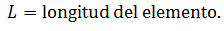
Matriz de rigidez en coordenadas globales para un determinado elemento i de una armadura, ki, ecuación 1-4.

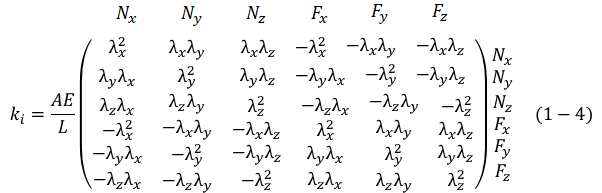
donde

• 𝐴 = área de la sección transversal del elemento
• 𝐸 = módulo de elasticidad del elemento
• 𝐿 = longitud del elemento
• 𝑁𝑥 , 𝑁𝑦 , 𝑁𝑦 = número de código del grado de libertad global asociado con el extremo  cercano 𝑁 en las direcciones 𝑥 , 𝑦 y z respectivamente del elemento en turno
• 𝐹𝑥 , 𝐹𝑦 , 𝐹z = número de código del grado de libertad global asociado con el extremo lejano 𝐹 en las direcciones 𝑥 , 𝑦 y z respectivamente del elemento en turno
• 𝜆𝑥 , 𝜆𝑦 , 𝜆z = cosenos directores

Partición de la matriz de rigidez, K, en sub matrices (K₁₁ , K₁₂ , K₂₁ y K₂₂ ), ecuación 1-5.

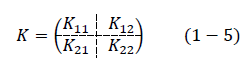
Vector de desplazamientos, D, ecuación 1-6.

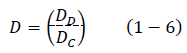
donde D_D es el vector de desplazamientos desconocidos y D_C  es el vector de desplazamientos conocidos. 

Vector de cargas, C, ecuación 1-7.

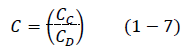
donde C_C es el vector de desplazamientos desconocidos y C_D  es el vector de desplazamientos conocidos. 

Ecuación matricial de la rigidez, ecuaciones 1-8 y 1-9.

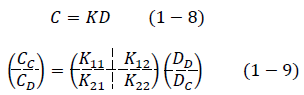
Subsistemas, ecuaciones 1-10 y 1-11.

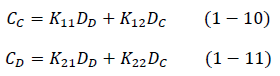
Atendemos al subsistema 1. Puesto que para esta armadura el vector de desplazamientos conocidos es un vector nulo dado que los soportes no se desplazan, D_C = 0. De ese modo, la ecuación 1 − 10 se reduce notablemente a

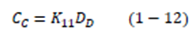
Desplazamientos desconocidos, ecuación 1-13.

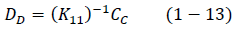
Con base en el subsistema 2, se obtienen las cargas desconocidas (reacciones en los soportes), ecuación 1-14.

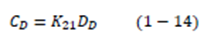
III. Ejemplo de aplicación empleando MATLAB y Excel

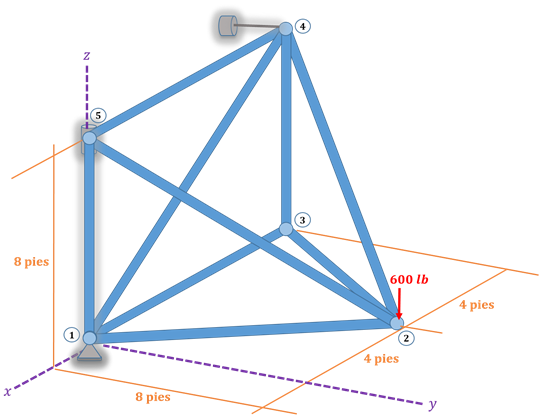
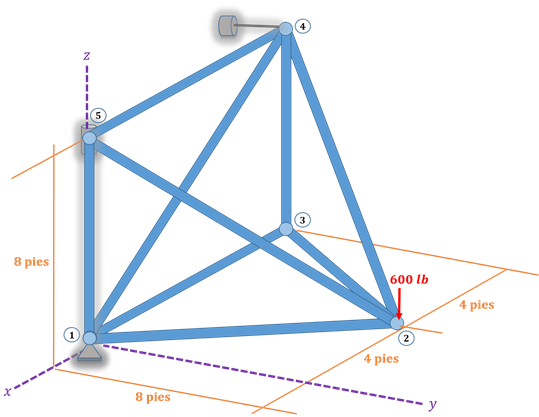
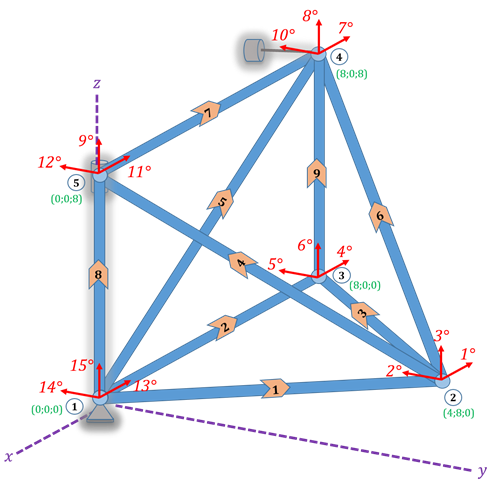
Instrucciones. Analizar la armadura mostrada en la figura empleando el Método Matricial de la Rigidez. Considere que todas las barras tienen una sección de 3cm x 3cm y que están hechas de acero con un módulo de elasticidad de 2.1*10⁷ ton/m²

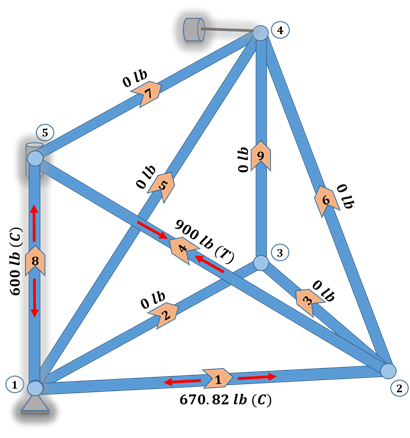
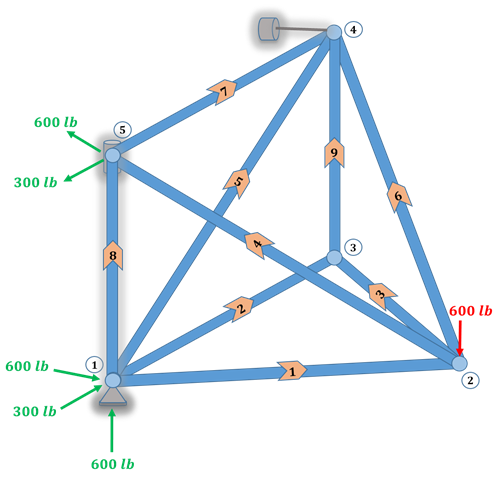
En la primera figura se muestran las fuerzas en las barras, mientras que en la segunda se muestran las reacciones en los soportes.

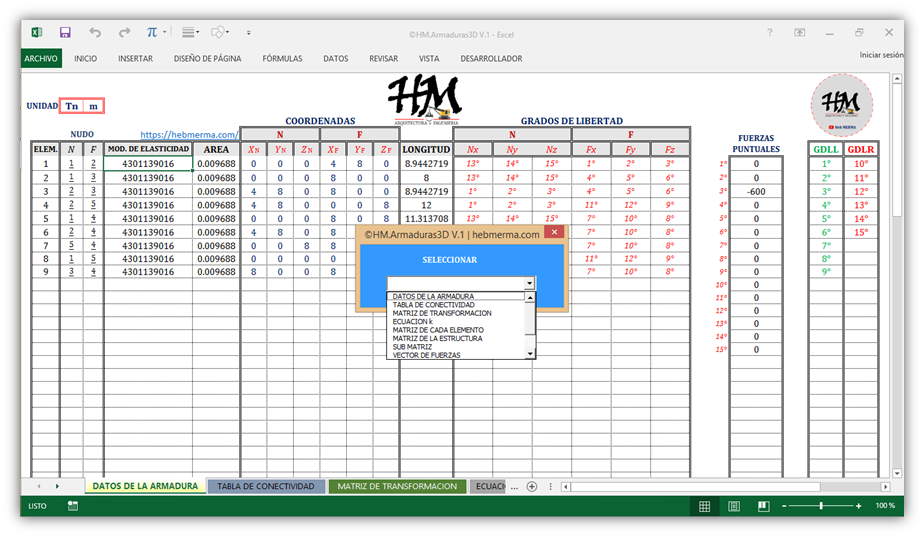
• 💻 CALCULOS:
• ☑️ TABLA DE CONECTIVIDAD
• ☑️ MATRIZ DE TRANSFORMACION
• ☑️ ECUACION k
• ☑️ MATRIZ DE CADA ELEMENTO
• ☑️ MATRIZ DE LA ESTRUCTURA
• ☑️ SUB MATRIZ k1
• ☑️ VECTOR DE CARGAS
• ☑️ DESPLAZAMIENTOS
• ☑️ FUERZAS INTERNAS
• ☑️ REACCIONES
• NOTA: Para llamar al índice presionar «Ctrl + H«

COMUNICADO: Para adquirir el Excel «©HM.Armaduras3D V.1» o «©HM.Armaduras3D V.2» comunicarse al WhatsApp +51 992 959 578.